图的基本操作

图的简介

图在数据结构中也是非常重要的逻辑结构之一，它比树（层次结构）要更为复杂。在图中，所有的链接点被称为“顶点”,图G由两个集合V(顶点Vertex)和E(边Edge)组成，定义为G=(V，E)。图可以说是树与线性表的进阶版，可以实现多对多逻辑关系。当然，也可以实现一对多关系。在下文中将为详细介绍图的相关概念与应用实现。

图的概念

名词解释

1. 邻接点。若无向图中顶点v,w之间存在一条边(v,w),称v,w互为邻接点。
2. 顶点的度。
   • 无向图：与某一顶点相关联的边的个数，称为该顶点的度。
   • 有向图：以某一顶点为弧头个数（简单来说都是只想该顶点的弧的个数）称之为该顶点的入度；以该顶点为弧尾的个数称之为该顶点的出度。
3. 简单路径。顶点不重复的路径成为简单路径。
4. 回路，首尾顶点相同的路径称为回路。
5. 简单回路，首尾顶点相同，但是其余任何一个顶点都不重复的回路，称之为简单回路。
6. 生成树。在一个连通图中，通过对于边的删除能够将其转变为一棵树，而这棵树被称之为生成树。

为了方便描述，现给出以下定义：

图G由顶点的集合和边的集合构成，记作：G=(V,E)
顶点 V（G）={顶点名1，……}
边是两顶点之间的连线，记作：E(G)={<顶点A，顶点B>，……}

有向图和无向图

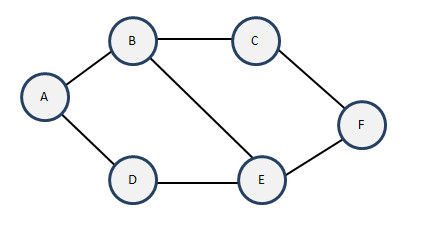
无向图是指两顶点直线只是单纯的至多由一根连接线相连的，对其方向没有限定，我们称这个连接线为边。一个顶点个数为n的无向图中，至多有（(n-1)*n/2）条边。

有向图则对于方向做出了限定，其连接线被称为弧，有弧尾和弧头之分，带箭头一端为弧头。无向图顶点的边数叫做度。有向图顶点分为入度和出度，入度是指该顶点拥有的弧头个数，出度的指该顶点拥有的弧尾个数。一个顶点个数为n的无向图中，至多有((n-1)*n)条弧。

邻接矩阵

它是图的二维数组存储方式。对于具有N个顶点的图来说，将会生成一个N行N列的二维数组。

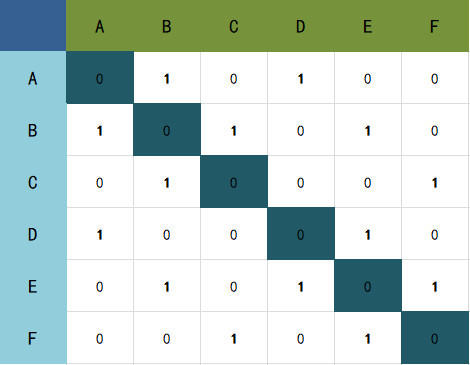
无向图的邻接矩阵是关于对角线对称的。列或者行中的1的个数代表该顶点的度。

而无向图的行中的1的个数代表该顶点的出度，而列中的1的个数代表该顶点的入度。

拓扑排序

在一个有向图中始终找入度为0的顶点，读出一个将该顶点中去除，依次将所有顶点都读出，最后的结构可能不止一种，当然也有可能没有结果。例如下图中的有向图的拓扑排序结果可以是：

1. ADBCEF
2. ABDECF
3. 等等……

图的遍历

所谓图的遍历是指，将图中所有顶点都不重复的访问一遍。

深度优先遍历（DBF）

深度优先遍历是遍历图的两大法宝之一，其核心思想按照我数据结构老师的话来说就是“一直往前走，直到走不动”，也就是说，在没访问过的顶点集合中，遇到能往下遍历的就往下遍历，当无法往下进行遍历时便回溯到上一个顶点，直到所有顶点都访问过为止。因为遍历时由代码实现的，为了更加容易理解实现，所以用邻接矩阵来说明深度优先遍历操作。

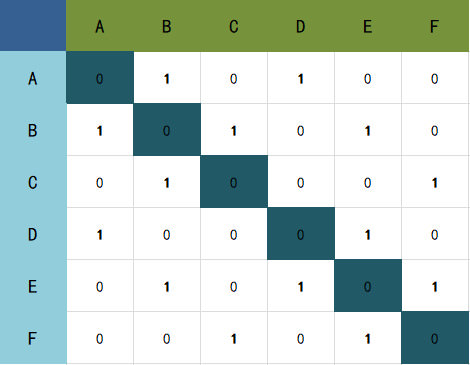
这个邻接矩阵就是上文中所介绍的。

例如这个邻接矩阵，我们设A为起点，其深度优先遍历的过程为：

1. 从A行中，第一个邻接点是B,所以访问B
2. 跳转到B行中，第一个未访问的邻接点是C,访问C
3. 跳转到C行时，第一个未访问的邻接点是F,所有访问F
4. 来到F行时，第一个未访问的邻接点是E,访问E
5. E行中，第一个未访问的邻接点是D

至此，我们的遍历工作就已经完成了。其结果是(A,B,C,F,E,D)

代码实现：

需要额外创建一个用于保存对应顶点是否被访问过的数组Visits[]。

//深度优先遍历
/*返回当前顶点的第一个邻接点的位置*/
int First(PGraph PG, int t) {
	if (PG == NULL)return -1;
	if (t < 0 || t >= PG->Vexnums)return -1;
	for (int i = 0; i < PG->Vexnums; i++)
		if (PG->AjMx[t][i] != INF && i != t)return i;
	return -1;
}
/*返回当前顶点相对于邻接点w之后的第一个邻接点的位置*/
int next(PGraph PG, int w, int t) {
	if (PG == NULL)return -1;
	if (t < 0 || t >= PG->Vexnums)return -1;
	if (w < 0 || w >= PG->Vexnums)return -1;
	for (int i = w+1; i < PG->Vexnums; i++)
		if (PG->AjMx[t][i] != INF && i != t)return i;
	return -1;
}
void DBF(PGraph PG, int *Visits, int T) {
	Visits[T] = 1;
	cout << PG->Vexs[T];
	for (int w = First(PG, T); w !=-1; w = next(PG, w, T)){
		if (Visits[w] == 0) 
			DBF(PG,Visits,w);
	}
}

int DBFmain(PGraph PG) {
	if (PG == NULL)return 0;
	int *Visits = new int[PG->Vexnums];
	for(int i=0;i<PG->Vexnums;i++)  //为浏览记录器Visits数组初始化为0
			Visits[i]=0;
	for (int i = 0; i < PG->Vexnums; i++){
		if (Visits[i] == 0)
			DBF(PG, Visits, i);
	}//图还存在”孤岛“或”孤岛群“，所以为了能够完整遍历所有顶点，要嵌套一个循环
	cout<<endl;
	delete []Visits;
	return 1;
}

广度优先遍历图

广度优先遍历，并不再像深度优先遍历那样一直往底走，而是类似于树的层次遍历那样，广度得一层一层往底部走。直到所有得顶点都遍历完毕。例如下图：

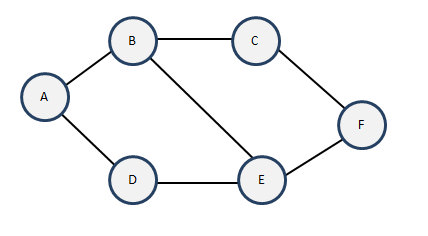
在该图中，我们默认以A为起点，开展如下步骤：

1. 因为A有两个未访问的邻接点，依次输出他们：B、D。
2. 在B中有两个未访问的邻接点，依次输出 C、E.
3. D中的E已经访问过了，所以无输出。
4. C中有一个未访问的邻接点，输出F。
5. E中的F也刚刚被访问过，所以依然无输出。
6. 所有顶点都已访问完毕，遍历结果为 ABDCEF

实际上广度优先遍历比深度优先遍历要更好理解，在代码实现也更加有意思。

BFS代码实现

第一个要解决的问题就是——如何做到知道某一顶点的将要访问的邻接点，然后再下去访问同层的下一顶点（广度优先的规则就是访问完同层顶点后才能按顺序去访问他们各自的下一层邻接顶点）。

例如在上面举得例子中，访问完B后如何让计算机知道B的两个邻接点C、E的情况下去把D访问掉，并且知道D有一个邻接点E,依次访问下去。

一种很巧妙的逻辑结构完美的解决了这个问题，它就是队列。由于队列具有先进先出的特性，所以我们只需要每次都把某顶点N的所有未访问邻接点都入队，然后将顶点N出队就可以了。代码如下，需要大家自己耐心琢磨：

/*广度优先遍历图*/
void BFS(PGraph PG){
	int Front,Rear; 
	Front=Rear=0;//初始化队头和队尾 
	int *queue=new int[PG->Vexnums]; //按广度优先顺序保存索引的队列 
	int *Visits=new int[PG->Vexnums];
	for(int i=0;i<PG->Vexnums;i++)Visits[i]=0; 
	
	for(int i=0;i<PG->Vexnums;i++){
		if(Visits[i]==0){
			cout<<PG->Vexs[i]; //输出起点或者另外连通子图的起点 
			Visits[i]=1;
			for(int w=First(PG,i);w!=-1;w=next(PG,w,i)){
				if(Visits[w]==0){
					Visits[w]=1;
					cout<<PG->Vexs[w];
					queue[++Rear]=w;  //输出当前顶点的邻接点，并按顺序将这些邻接点的索引入队 
				}
			}
		}
		while(Front!=Rear){ 
			int k=queue[++Front];//依次出队，输出该顶点下的所有未访问过的邻接点，并将他们的索引入队 
			for(int w=First(PG,k);w!=-1;w=next(PG,w,k)){
				if(Visits[w]==0){
					Visits[w]=1;
					cout<<PG->Vexs[w];
					queue[++Rear]=w;
				}
			}
		}
	}
	delete []queue;
	delete []Visits;
}

最小生成树

在一个带权连通图中，生成的路径之和最小的一棵生成树，被称之为最小生成树。实现最小生成树有两种方法，其中一种是易于理解的Prim算法，另外一种是根据贪心算法实现的Kruskal算法。

Prim算法实现最小生成树

其基本思想是：在一个初始化时只有起点的生成树E中，找这棵生成树中所有顶点连接边权值最小的邻接点，并且不能造成回路，直到这张连通图中的所有顶点都连接到这棵生成树之中为止。ps:让我想到了那句魔性广告词：开局只有一条狗，装备全靠打……

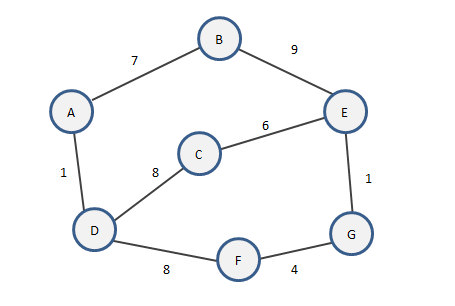
例如上图中的带权连通图，我们设起点为A，设生成树为E:

1. 初始时，E中只有A顶点
2. 最小邻接点有D，将D加入到E中E{<A,D,1>}
3. 最小邻接点有B,E更新为E{<A,D,1>,<A,B,7>}
4. 最小邻接点有C和F,优先选择C。E更新为E{<A,D,1>,<A,B,7>,<D,C,8>}
5. 最小邻接点有E。E加入<C,E,6>
6. 最小邻接点有G。E加入<E,G,1>
7. 最小邻接点有F。E加入<G,F,4>

最终得到的最小生成树为

E{
<A,D,1>
<A,B,7>
<D,C,8>
<C,E,6>
<E,G,1>
<G,F,4>
}

而最小生成树的带权路径之和为27。

如果还是感觉上文中的式子不太清晰，那就再上图：

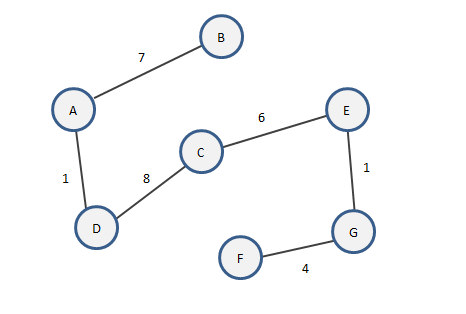
Kruskal算法实现最小生成树

Kruskal算法的思想是：在带权连通图中，再没有找过的边中找权值最小的边且不能造成回路，直到生成树连接到所有的顶点为止。
上图中的例子来说，依然设生成树为E：

1. 权值最小的边有<A,D,1>和<E,G,1>,且两条边不会造成回路。分别加入到E中。
2. 未选出的边中权值最小的边有<F,G,4>。加入到E中。
3. 权值最小的边有<C,E,6>,加入到E中。
4. 权值最小的边有<A,B,7>,加入到E中。
5. 权值最小的边有<D,C,8>和<D,E,8>,可以任选一条，但是注意不能两条都选，会造成回路。我们选择<D,C,8>加入到E中。

最终通过Kruskal算法得到的最小生成树为：

E{
<A,D,1>
<E,G,1>
<F,G,4>
<C,E,6>
<A,B,7>
<D,C,8>