哈夫曼树

发表于 | 更新于 | 分类于 | 评论数：
本文字数： 18k | 阅读时长 ≈ 16 分钟

哈夫曼(Huffman)树，又称为最优二叉树，是带权路径长度（wpl）最短的二叉树。

一般我们要做的事分为三步:

  1. 构建哈夫曼树
  2. 求WPL值
  3. 求哈夫曼编码

构造哈夫曼树

  1. 将所有左，右子树都为空的作为根节点。
  2. 在森林中选出两棵根节点的权值最小的树作为一棵新树的左，右子树，且置新树的附加根节点的权值为其左，右子树上根节点的权值之和。注意，左子树的权值应小于右子树的权值。
  3. 从森林中删除这两棵树，同时把新树加入到森林中。
  4. 重复2，3步骤，直到森林中只有一棵树为止，此树便是哈夫曼树。

下面是构建哈夫曼树的图解过程：

WPL值的求法

事实上wpl有两种求法

  1. 将哈夫曼树的所有分支节点的权值相加就是我们要求的wpl值
  2. 将哈夫曼树中的所有叶子节点的权值于路径长度的乘积相加也是我们要求的wpl值

例如上图的wpl值就是48

哈夫曼编码

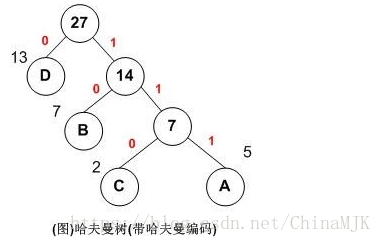
用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。树中从根到每个叶子节点都有一条路径，对路径上的各分支约定指向左子树的分支表示”0”码，指向右子树的分支表示“1”码，取每条路径上的“0”或“1”的序列作为各个叶子节点对应的字符编码，即是哈夫曼编码。

就拿上图例子来说：

A，B，C，D对应的哈夫曼编码分别为：111，10，110，0

用图说明如下：

img

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <iostream>    
#include<cstdio>    
#include<cstdlib>    
using namespace std;    
typedef struct BTreeNode    
{    
    int  data;    
    struct BTreeNode* left;    
    struct BTreeNode* right;    
}btreenode;    
        
//建立哈夫曼树    
btreenode *CreateHuffman(int a[],int n)  
{    
    int i;    
    btreenode *s[n+1], *ss;    
    for(int i = 0;i<n;i++){    
        s[i] = new btreenode;  //初始化s指针数组，使每个指针元素指向a数组中对应的元素结点    
        s[i]->data = a[i];   //将树拆成森林，每棵树都只有一个根节点    
        s[i]->left = s[i]->right = NULL;    
    }    
      
    for(int i  = 1;i<n;i++){        //进行 n-1次循环建立哈夫曼树    
           int k = -1,t;           //k表示森林中具有最小权值的树根结点的下标，t为次最小的下标    
        for(int j = 0;j<n;j++){   //k初始指向森林中第一棵树，t指向第二棵    
                if(s[j]&&k==-1){    
                   k = j;    
                   continue;    
                }    
                if(s[j]){    
                    t =  j;    
                    break;    
                }    
        }    
            for(int i = t;i<n;i++){   //从当前森林中求出最小权值树和次最小 ；    
            if (s[i]){    
                if(s[i]->data<s[k]->data){        //比最小树小   
                    t = k;    
                    k = i;    
                }    
                else if(s[i]->data<s[t]->data){  //比次小树小   
                    t = i;    
                }    
                else{    
                    ;    
                }    
            }    
        }    
           //由最小权值树和次最小权值树建立一棵新树，ss指向树根结点(以后依次建立)    
           ss  = new btreenode;     //ss = (btreenode *)malloc(sizeof(btreenode))            
           ss->data =   s[k]->data+s[t]->data;    
           ss->left =   s[k];    
           ss->right =  s[t];    
           s[k] =  ss;  //关键点:将ss赋给s[k](k为上述找到的最小树下标,但这是s[k]代表的值已改变，同时把s[t]失效的置空,    
                       //在这里起向下一个判断的作用if(s[j]){t = j;break;}    
           s[t] = NULL;    
    }    
        return ss;   
        free(s);   //释放分配空间    
}     
//求哈夫曼树的带权路径长度        
int WeightPathLength(btreenode* FBT, int len){          //参数len为树的层数   
    if(!FBT){    
            return 0;    
    }    
    else{    
        if(FBT->left ==NULL&&FBT->right ==NULL)//访问到叶子结点    
            return FBT->data*len;    
        else{               //访问到非叶子结点，进行递归调用，返回左右子树的带权路径长度之和，len递增    
            return  WeightPathLength(FBT->left,len+1)+WeightPathLength(FBT->right,len+1);//一定要记得加1    
        }    
    }       
}    
   
//哈夫曼编码    
void HuffManCoding(btreenode* FBT, int len){   //参数len为树的层数   
    static int a[20];                        //定义静态数组a，保存每个叶子的编码，数组长度至少是树深度减1   
    if(FBT){                                //访问到叶子结点时输出其保存在数组a中的0和1序列编码    
        if(FBT->left == NULL&&FBT->right == NULL){    
            printf("结点权值为%d的编码:",FBT->data);    
             for(int i = 0;i<len;i++){    
                 printf("%d",a[i]);    
            }    
                printf("\n") ;    
        }    
        else{    //访问到非叶子结点时分别向左右子树递归调用，并把分支上的0、1编码保存到数组    
                //a的对应元素中，向下深入一层时len值增1    
               a[len] = 0;    
               HuffManCoding(FBT->left,len+1);    
               a[len] = 1;    
               HuffManCoding(FBT->right,len+1);    
            }    
    }    
}    
      
int main(){    
    btreenode *s;    
    int n;    
    printf("从键盘输入待构造的哈夫曼树中带权叶子结点数n：");    
    while(true){    
        scanf("%d",&n);    
        if(n>0){    
            break;    
        }    
        else{    
            printf("-------输入不合法,请重新输入!!\n");    
        }    
    }    
    int *a = (int *)malloc(n *sizeof(int));    
    printf("从键盘输入%d个整数作为权值:",n);    
    for (int i = 0; i < n; i++)    
        scanf("%d", &a[i]);    
    s = CreateHuffman(a,n);    
      
    printf("哈夫曼树的带权路径长度：");    
    printf("%d\n", WeightPathLength(s, 0));    
      
    printf("树中每个叶子结点的哈夫曼编码：\n");    
    HuffManCoding(s,0);    
      
    return 0;    
}
0%